Clique para aprender os procedimentos necessários para realizar a divisão entre dois polinômios!
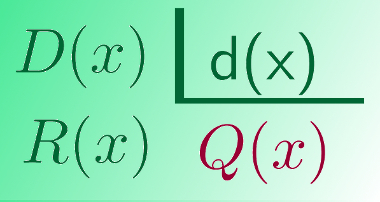
Dados dois polinômios, representados por A(x) e B(x), é possível realizar a divisão de A(x) por B(x) sempre que o grau do polinômio A(x) for maior que o de B(x). Essa divisão acontece de modo similar à de números inteiros.
→ Método usado para dividir polinômios
Para dividir polinômios utilize o método da chave e siga o mesmo passo a passo da divisão de números inteiros. Como o método usado é o mesmo, a denominação dos polinômios também será igual. Observe:

D(x) é o dividendo;
d(x) é o divisor;
Q(x) é o quociente;
R(x) é o resto.
O procedimento para dividir polinômios é praticamente idêntico à divisão de números inteiros, variando apenas nos detalhes.

Dessa maneira, é necessário procurar um polinômio que, multiplicado pelo divisor, tenha o dividendo ou uma boa aproximação dele como resultado. A diferença entre esse produto e o dividendo é o resto.
→ Passo a passo para dividir polinômios
Para dividir polinômios, observe o passo a passo a seguir:
1) Escreva os polinômios na forma do método da chave, reorganizando seus termos na ordem decrescente do grau de seus monômios (se necessário);
2) Procure por um monômio q(x) que, multiplicado pelo primeiro monômio do divisor, tenha exatamente o primeiro monômio do dividendo como resultado;
3) Multiplique q(x) pelo divisor e coloque o resultado abaixo do dividendo trocando todos os sinais de seus termos;
4) “Desça” os termos restantes do divisor;
5) Repita o procedimento para o novo dividendo até que o grau do dividendo seja menor que o grau do divisor. Quando isso acontecer, não será mais possível dividir os polinômios.
Exemplos
1º) Divida D(x) = – 8x + x2 + 16 por d(x) = x – 4
Solução:
Passo 1:
![]()
Reorganizando os polinômios na ordem decrescente do grau de seus monômios teremos:
![]()
Passo 2:
![]()
Pois x·x = x2. Observe que o monômio q(x) = x.
Passo 3:

Observe que a multiplicação de x por x – 4 é x2 – 4x, entretando, trocamos os sinais dos termos desse polinômio para colocá-lo abaixo do dividendo porque estamos realizando uma subtração.
Passo 4:

Passo 5: apenas repetiremos todos os procedimentos anteriores até que o grau do resto seja inferior ao grau do divisor. Observe:

O resultado Q(x) da divisão de D(x) por d(x) é Q(x) = x – 4
2º) Divida D(x) = 6x4 – 10x3 + 9x2 + 10x – 4 por d(x) = 2x2 – 4x + 5
Solução:
Passo 1:
![]()
Passo 2:
![]()
Passo 3:

Passo 4:

Passo 5:

O resultado é Q(x) = 3x2 + x – 1 e o resto é R(x) = x + 5.
Por Luiz Paulo Moreira
Graduado em Matemática
Aproveite para conferir nossas videoaulas sobre o assunto: